rotary position embeddings (rope)
Rotary Position Embeddings (RoPE) is a position encoding method which has found its way in several popular transformer architectures: LLaMA 3, Gemma, GPT-J and many more.
Here is a short summary from the abstract of the paper:
“The proposed RoPE encodes the absolute position with a rotation matrix and meanwhile incorporates the explicit relative position dependency in self-attention formulation. Notably, RoPE enables valuable properties, including the flexibility of sequence length, decaying inter-token dependency with increasing relative distances, and the capability of equipping the linear self-attention with relative position encoding.”
In this post, I provide a brief overview of RoPE and the motivation behind it.
We will first start off with how other positional encoding methods work. Next, we provide the necessary background and derivation of RoPE. Finally, we will take a step back and discuss the high-level intuition behind RoPE and why it seems to work so well in practice.
Related Work
Let $\mathbb{S}_N = \{ w_i \}_{i=1}^N$ be a sequence of $N$ input tokens with $w_i$ being the $i$-th token. The corresponding word embedding of $\mathbb{S}_N $ is denoted as $\mathbb{E}_N = \{ \bf{x}_i\}_{i=1}^N $, where $\bf{x}_i \in \mathbb{R}^d $ is the $d$-dimensional embedding of $w_i$ without position information.
$$ \begin{align} \bf{q}_m &= f_q (\bf{x}_m, m) \notag \\ \bf{k}_n &= f_k (\bf{x}_n, n) \label{eq:kqv} \\ \bf{v}_n &= f_v (\bf{x}_n, n) \notag \end{align} $$$$ \begin{align} a_{m, n} &= \frac{\exp \left(\frac{\bf{q}_m^T \bf{k}_n}{\sqrt{d}} \right)}{\sum_{j=1}^N \exp \left( \frac{\bf{q}_m^T \bf{k}_j}{\sqrt{d}} \right)} \label{eq:attention}\\ \bf{o}_m &= \sum_{n=1}^N a_{m, n} \bf{v}_n \end{align} $$Most approaches to positional encoding can be grouped in two categories: absolute and relative.
Absolute position embedding
$$ \begin{align} f_{\{q, k, v \}} (\bf{x}_i, i) &:= \bf{W}_{\{q, k, v \}} (\bf{x}_i + \bf{p}_i) \end{align} $$where $ \bf{p}_i $ is a $d$-dimensional positional encoding vector.
Previous work Devlin et al. (2019), Lan et al. (2020), Clark et al. (2020), Radford et al. (2019), Radford and Narasimhan (2018) introduced the use of a set of trainable vectors $ \bf{p}_i \in \{ \bf{p}_t \}_{t=1}^L$, where $L$ is the maximum sequence length.
$$ \begin{align} \begin{cases} \bf{p}_{i, 2t} &= \sin ( k/10000^{2t/d} ) \\ \bf{p}_{i, 2t+1} &= \cos ( k/10000^{2t/d}) \end{cases} \end{align} $$in which $\bf{p}_{i, 2t}$ is the $2t$-th element of the $d$-dimensional vector $\bf{p}_i$.
Relative position embedding
$$ \begin{align} f_q \left( x_m \right) &:= \bf{W}_q \bf{x}_m \notag \\ f_k \left(x_n, n \right) &:= \bf{W}_k (x_n + \tilde{\bf{p}}_r^k) \\ f_v \left(x_n, n \right) &:= \bf{W}_v (x_n + \tilde{\bf{p}}_r^v) \notag \end{align} $$where $\tilde{\bf{p}}_r^k$ and $\tilde{\bf{p}}_r^v$ are trainable relative position embeddings. Note that $r = \text{clip} (m-n, r_{\text{min}}, r_{\text{max}})$ represents the relative distance between position $m$ and $n$. The clipping is done under the hypothesis that precise relative position information is not useful beyond a certain distance.
$$ \begin{align} \bf{q}_m^T \bf{k}_n &= \bf{x}_m^T \bf{W}_q^T \bf{W}_k \bf{x}_n + \bf{x}_m^T \bf{W}_q^T \bf{W}_k \bf{p}_n + \bf{p}_m^T \bf{W}_q^T \bf{W}_k \bf{x}_n + \bf{p}_m^T \bf{W}_q^T \bf{W}_k \bf{p}_n \end{align} $$$$ \begin{align} \bf{q}_m^T \bf{k}_n &= \bf{x}_m^T \bf{W}_q^T \bf{W}_k \bf{x}_n + \bf{x}_m^T \bf{W}_q^T \tilde{\bf{W}}_k \tilde{\bf{p}}_{m-n} + \bf{u}^T \bf{W}_q^T \bf{W}_k \bf{x}_n + \bf{v}^T \bf{W}_q^T \tilde{\bf{W}}_k \tilde{\bf{p}}_{m-n} \end{align} $$There are several other variations, but we live it to the reader to explore them further.
Theoretical Explanation of RoPE
$$ \begin{align} \langle f_q(x_m, m), f_k(x_n, n) \rangle &= g(\bf{x}_m, \bf{x}_n, m-n) \end{align} $$and outputs a dot product which incorporates both the content-based and location-based information.
Complex numbers
Before we dive into the derivation of RoPE, let’s first introduce complex numbers and their properties.
A complex number is a number that can be expressed in the form $a + bi$, where $a$ and $b$ are real numbers, and $i$ is the imaginary unit. The imaginary unit satisfies the property $i^2 = -1$.
Complex numbers can be represented in several forms:
- Rectangular (Cartesian) form: $z = a + bi$, where $a$ is the real part and $b$ is the imaginary part.
- Polar form: $z = r (\cos \theta + i \sin \theta)$, where $r$ is the magnitude and $\theta$ is the angle.
- Exponential form: $z = r e^{i \theta}$, where $r$ is the magnitude and $\theta$ is the angle. This form is directly related to the polar form due to Euler’s formula: $e^{i \theta} = \cos \theta + i \sin \theta$.
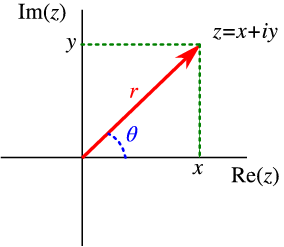
A complex number can visually be represented as a vector in the complex plane, where the real part is the x-coordinate and the imaginary part is the y-coordinate. Conversly, in the polar form, the magnitude of a complex number is the distance from the origin to the point in the complex plane, while the angle is the angle between the positive x-axis and the vector.
Since all forms are equivallent, we can easily convert between them:
- To go from rectangular to polar form: $$ \begin{align*} r &= \sqrt{a^2 + b^2} \\ \theta &= \arctan \left( \frac{b}{a} \right) \\ z &= r (\cos \theta + i \sin \theta) \end{align*} $$
- To go from the polar to the exponential form, we can directly utilize Euler’s formula: $$ \begin{align*} z &= r (cos \theta + i \sin \theta) = r e^{i \theta} \end{align*} $$
This is going to be crucial for the derivation of RoPE.
Derivation of RoPE
First, we consider the case when the embeddings are two-dimensional, i.e. $d=2$, and later provide a generalized form of the RoPE for higher dimensions.
$$ \begin{align} \bf{q}_m &= f_q (\bf{x}_m, m) \\ \bf{k}_n &= f_k (\bf{x}_n, n) \end{align} $$where the subscripts of $\bf{q}_m$ and $\bf{k}_n$ denote the encoded positional information.
$$ \begin{align} \bf{q}_m^T \bf{k}_n = \langle f_q (\bf{x}_m, m), f_k (\bf{x}_n, n) \rangle = g(\bf{x}_m, \bf{x}_n, n-m) \label{eq:g_inner_product} \end{align} $$$$ \begin{align} \bf{q} &= f_q (\bf{x}_q, 0) \label{eq:initial_q_functional} \\ \bf{k} &= f_k (\bf{x}_k, 0) \label{eq:initial_k_functional} \end{align} $$which can be read as the vectors with empty position information encoded.
Given these settings, the authors of RoPE aim to find a solution to $f_q$ and $f_k$.
$$ \begin{align} f_q (\bf{x}_q, m) &= R_q(\bf{x}_q, m) e^{i\Theta_q(\bf{x}_q, m)} \label{eq:f_def} \\ f_k (\bf{x}_k, n) &= R_k(\bf{x}_k, n) e^{i\Theta_k(\bf{x}_k, n)} \\ g(\bf{x}_q, \bf{x}_k, n-m) &= R_g(\bf{x}_q, \bf{x}_k, n-m) e^{i\Theta_g(\bf{x}_q, \bf{x}_k, n-m)} \end{align} $$$$ \begin{align} R_q(\bf{x}_q, m) R_k(\bf{x}_k, n) = R_g(\bf{x}_q, \bf{x}_k, n-m) \label{eq:rope_magnitude_relation} \\ \Theta_k (\bf{x}_k, n) - \Theta_q (\bf{x}_q, m) = \Theta_g (\bf{x}_q, \bf{x}_k, n-m) \label{eq:rope_angle_relation} \end{align} $$Note: Since we are operating in the complex space, the inner product involves complex conjugation, which is the reason why the angles are subtracted.
$$ \begin{align} \bf{q} &= \Vert \bf{q} \Vert e^{i \Theta_q} = R_q(\bf{x}_q, 0) e^{i \Theta_q(\bf{x}_q, 0)} \label{eq:initial_q} \\ \bf{k} &= \Vert \bf{k} \Vert e^{i \Theta_k} = R_k(\bf{x}_k, 0) e^{i \Theta_k(\bf{x}_k, 0)} \end{align} $$where $\Vert \bf{q} \Vert$, $\Vert \bf{k} \Vert$ and $\Theta_q$, $\Theta_k$ are the magnitudes and angles of the vectors $\bf{q}$ and $\bf{k}$ respectively.
$$ \begin{align} R_q (\bf{x}_q, m) R_k(\bf{x}_k, m) &= R_g(\bf{x}_q, \bf{x}_k, 0) &\text{(from Equation \eqref{eq:rope_magnitude_relation})} \\ &= R_q(\bf{x}_q, 0) R_k(\bf{x}_k, 0) &\text{(also Equation \eqref{eq:rope_magnitude_relation} when $m=n=0$)} \\ &= \Vert \bf{q} \Vert \Vert \bf{k} \Vert &\text{(from the initial conditions)}\\ \end{align} $$$$ \begin{align} \Theta_k(\bf{x}_k, m) - \Theta_q(\bf{x}_q, m) &= \Theta_g(\bf{x}_q, \bf{x}_k, 0) &\text{(from Equation \eqref{eq:rope_angle_relation})} \\ &= \Theta_k(\bf{x}_k, 0) - \Theta_q(\bf{x}_q, 0) &\text{(also Equation \eqref{eq:rope_angle_relation} when $m=n=0$)} \\ &= \Theta_k - \Theta_q &\text{(from the initial conditions)} \end{align} $$$$ \begin{align} R_q(\bf{x}_q, m) &= R_q(\bf{x}_q, 0) = \Vert \bf{q} \Vert \label{eq:radial_value}\\ R_k(\bf{x}_k, m) &= R_k(\bf{x}_k, 0) = \Vert \bf{k} \Vert \\ R_g(\bf{x}_q, \bf{x}_k, n-m) &= R_g(\bf{x}_q, \bf{x}_k, 0) = \Vert \bf{q} \Vert \Vert \bf{k} \Vert \end{align} $$which can be interpreted as the radial functions $R_q$, $R_k$ and $R_g$ are independent from the positional information.
$$ \begin{align} \Theta_q(\bf{x}_q, m) - \Theta_q &= \Theta_k(\bf{x}_k, m) - \Theta_k \end{align} $$$$ \begin{align} \Theta_f := \Theta_q = \Theta_k \end{align} $$$$ \begin{align} \Phi(m) &= \Theta_f(\bf{x}_{\{q, k\}}, m) - \Theta_{\{q, k\}} \\ \implies \Theta_f(\bf{x}_{\{q, k\}}, m) &= \Phi(m) + \Theta_{\{q, k\}} \label{eq:angular_phi_relation} \end{align} $$$$ \begin{align} \Theta_k(\bf{x}_k, m+1) - \Theta_q(\bf{x}_q, m) &= \Theta_g(\bf{x}_q, \bf{x}_k, m+1-m) \\ \implies \left( \Phi(m+1) + \Theta_k \right) - \left( \Phi(m) + \Theta_q \right) &= \Theta_g(\bf{x}_q, \bf{x}_k, 1) \\ \implies \Phi(m+1) - \Phi(m) &= \Theta_g(\bf{x}_q, \bf{x}_k, 1) + \Theta_q - \Theta_k \end{align} $$$$ \begin{align} \Phi(m) = m \Theta + \gamma \label{eq:angular_arithmetic} \end{align} $$where $\Theta$ is the common difference and $\gamma$ is the initial term.
$$ \begin{align} f_q(\bf{x}_q, m) &= R_q(\bf{x}_q, m) e^{i \Theta_q(\bf{x}_q, m)} &\text{(from Equation \eqref{eq:f_def})} \\ &= \Vert \bf{q} \Vert e^{i \Theta_q (\bf{x}_q, m)} &\text{(from Equation \eqref{eq:radial_value})} \\ &= \Vert \bf{q} \Vert e^{i (\Phi(m) + \Theta_q)} &\text{(from Equation \eqref{eq:angular_phi_relation})} \\ &= \Vert \bf{q} \Vert e^{i (m \Theta + \gamma + \Theta_q)} &\text{(from Equation \eqref{eq:angular_arithmetic})} \\ &= \Vert \bf{q} \Vert e^{i \Theta_q} e^{i (m \theta + \gamma)} \\ &= \bf{q} e^{i (m \theta + \gamma)}&\text{(from Equation \eqref{eq:initial_q})} \label{eq:rope_f_q} \end{align} $$$$ \begin{align} f_k(\bf{x}_k, m) &= \Vert \bf{k} \Vert e^{i (\Theta_k + n \theta + \gamma)} = \bf{k} e^{i (n \theta + \gamma)} \label{eq:rope_f_k} \end{align} $$Notice that in the above formulation, the authors slightly abuse the notation by jointly using complex numbers and vectors. Nevertheless, we proceed with this notation as it is more intuitive.
$$ \begin{align} \bf{q} &= f_q (\bf{x}_q, 0) = \bf{W}_q \bf{x}_q \label{eq:initial_q_attention} \\ \bf{k} &= f_k (\bf{x}_k, 0) = \bf{W}_k \bf{x}_k \label{eq:initial_k_attention} \end{align} $$where $\bf{W}_q$, $\bf{W}_k$ are the trainable projection matrices used in the self-attention mechanism.
$$ \begin{align} f_q(\bf{x}_m, m) &= \left( \bf{W}_q \bf{x}_m\right) e^{i m \theta} \label{eq:rope_f_q_final} \\ f_k(\bf{x}_n, n) &= \left( \bf{W}_k \bf{x}_n\right) e^{i n \theta} \label{eq:rope_f_k_final} \end{align} $$$$ \begin{align} f_{\{q, k\}} (\bf{x}_m, m) &= \begin{pmatrix} \cos m \theta & -\sin m \theta \\ \sin m \theta & \cos m \theta \end{pmatrix} \begin{pmatrix} \bf{W}_{\{q, k\}}^{(1, 1)} & \bf{W}_{\{q, k\}}^{(1, 2)} \\ \bf{W}_{\{q, k\}}^{(2, 1)} & \bf{W}_{\{q, k\}}^{(2, 2)} \end{pmatrix} \begin{pmatrix} \bf{x}_m^{(1)} \\ \bf{x}_m^{(2)} \end{pmatrix} \end{align} $$Therefore, incorporating relative positional embeddings is straightforward:
Simply rotate the affine-transformed word embedding vector by amount of angle multiples proportional to its position index.
General form
$$ \begin{align} f_{\{q, k\}} (\bf{x}_m, m) &= \bf{R}_{\Theta, m}^d \bf{W}_{\{q, k\}} \bf{x}_m \end{align} $$$$ \begin{align} \bf{R}_{\Theta, m}^d = \begin{pmatrix} \cos m \theta_1 & -\sin m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m \theta_1 & \cos m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m \theta_2 & -\sin m \theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m \theta_2 & \cos m \theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d/2} & -\sin m \theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d/2} & \cos m \theta_{d/2} \\ \end{pmatrix} \end{align} $$$$ \begin{align} \Theta = \{\theta_i = 10000^{-2(i-1)/d} , i \in \{1, 2, \dots, d/2 \}\} \end{align} $$$$ \begin{align} \bf{q}_m^T \bf{k}_n &= \left( \bf{R}_{\Theta, m}^d \bf{W}_q \bf{x}_m \right)^T \left( \bf{R}_{\Theta, n}^d \bf{W}_k \bf{x}_n \right) \\ &= \bf{x}_m^T \bf{W}_q^T \bf{R}_{\Theta, n-m}^d \bf{W}_k \bf{x}_n \end{align} $$where $ \bf{R}_{\Theta, n-m}^d = (\bf{R}_{\Theta, m}^d)^T \bf{R}_{\Theta, n}^d $.
To understand why the equality of the rotary matrices holds, remember that any rotation matrix $\bf{R}$ is an orthogonal matrix, therefore $\bf{R}^T = \bf{R}^{-1}$.
Therefore, the chain of rotations $ (\bf{R}_{\Theta, m}^d)^{T} \bf{R}_{\Theta, n}^d = (\bf{R}_{\Theta, m}^d)^{-1} \bf{R}_{\Theta, n}^d $ can be read as: first go from the n “steps” counter clockwise, and then go back m “steps” clockwise. This is eqivalent to going $(n-m)$ steps counter clockwise, i.e. $\bf{R}_{\Theta, n-m}^d$
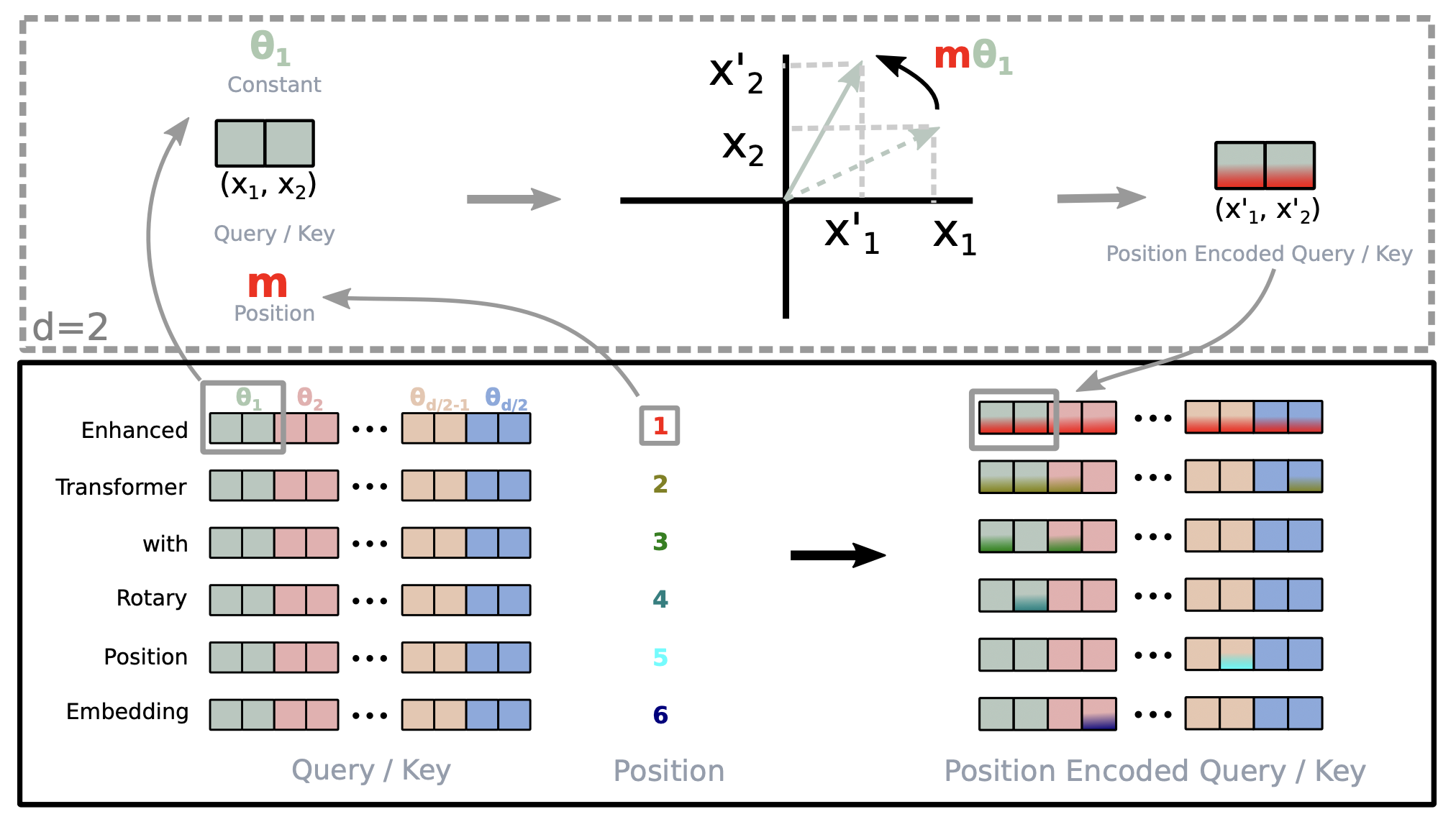
Above is a visual representation of RoPE (source: original paper).
Efficient computation
Note that since the rotation matrix $\bf{R}_{\Theta, n-m}^d$ is sparse, it is not computationally efficient to perform this matrix multiplication directly.
$$ \begin{align} \bf{R}_{\Theta, n-m}^d \bf{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots \\ x_{d-1} \\ x_d \end{pmatrix} \odot \begin{pmatrix} \cos m\theta_1 \\ \cos m\theta_1 \\ \cos m\theta_2 \\ \cos m\theta_2 \\ \vdots \\ \cos m\theta_{d/2} \\ \cos m\theta_{d/2} \end{pmatrix} + \begin{pmatrix} -x_2 \\ x_1 \\ -x_4 \\ x_3 \\ \vdots \\ -x_d \\ x_{d-1} \end{pmatrix} \odot \begin{pmatrix} \sin m\theta_1 \\ \sin m\theta_1 \\ \sin m\theta_2 \\ \sin m\theta_2 \\ \vdots \\ \sin m\theta_{d/2} \\ \sin m\theta_{d/2} \end{pmatrix} \end{align} $$which only involves two element-wise multiplications and one addition.
Conclusion
In summary:
- RoPE encodes absolute positional information by rotating each token’s embeddings with a position-specific rotation matrix $ \bf{R}_{\Theta, m}^d $, where $m$ is the token’s position.
- RoPE also encodes relative positional information, naturally derived from the inner products of the rotated embeddings in the self-attention mechanism: $ \bf{q}_m^T \bf{k}_n = \bf{x}_m^T \bf{W}_q^T \bf{R}_{\Theta, n-m}^d \bf{W}_k \bf{x}_n $.
Appendix
Visualization of RoPE
In this section, we provide several visualizations in order to better understand the RoPE mechanism.
First, let us pre-compute the frequencies for several token positions and embedding dimension pairs:
import matplotlib.pyplot as plt
import seaborn as sns
import torch
def precompute_freqs_cis(dim: int, num_tokens: int, theta: float = 10000.0):
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
t = torch.arange(num_tokens, device=freqs.device, dtype=torch.float32)
freqs = torch.outer(t, freqs)
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
return freqs_cis
dim = 512
num_tokens = 128
theta = 10000.0
token_idx = 3
freqs_cis = precompute_freqs_cis(dim, num_tokens, theta)
print(f"Shape: {freqs_cis.shape}, Dtype: {freqs_cis.dtype}")
print(f"First 10 elements (in degrees) for freqs at pos {token_idx}:")
print(torch.rad2deg(torch.angle(freqs_cis[token_idx, :]))[:10])
Shape: torch.Size([128, 256]), Dtype: torch.complex64
First 10 elements (in degrees) for freqs at pos 3:
tensor([171.8873, 165.8131, 159.9536, 154.3011, 148.8483, 143.5883, 138.5141,
133.6192, 128.8973, 124.3423])
Let us peek at all the frequencies of rotations for the token at position 3:
plt.plot(torch.rad2deg(torch.angle(freqs_cis[token_idx, :])).cpu().numpy())
plt.xlabel('Index of pair in embedding dimension')
plt.ylabel('Rotation (degrees)')
plt.title(f'Rotation angles for token {token_idx}')
plt.show()
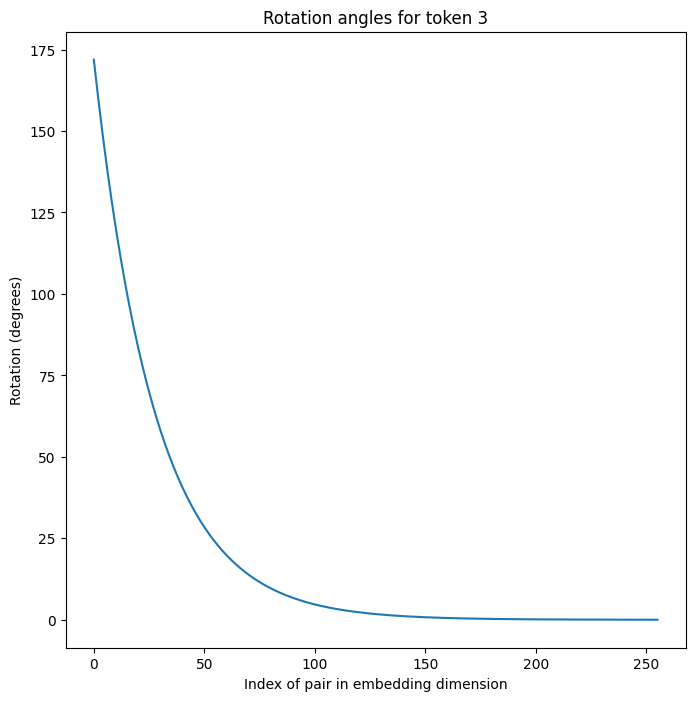
More precisely, in the plot above, we are looking at how much each pair of dimensions is rotated counter-clockwise for the token at position 3.
Therefore, if we rotate a vector whose initial position is $(1, 0)$ using the angles of rotation above:
vec = torch.tensor([1, 0], dtype=torch.float32)
vec_complex = torch.view_as_complex(vec)
freqs_for_token = freqs_cis[token_idx, :]
rotated_vec = vec_complex * freqs_for_token # multiplication in complex space = rotation
plt.figure(figsize=(12, 12))
for i in range(64):
plt.plot([0, rotated_vec[i].real], [0, rotated_vec[i].imag], color='blue')
plt.annotate(f'{i+1}', (rotated_vec[i].real, rotated_vec[i].imag), color='red')
plt.plot([0, 1], [0, 0], color='black')
plt.annotate('0', (1, 0), color='red')
plt.axis('equal')
plt.legend()
plt.title(f'Rotated vector at token {token_idx}')
plt.show()
We get the following visualization:
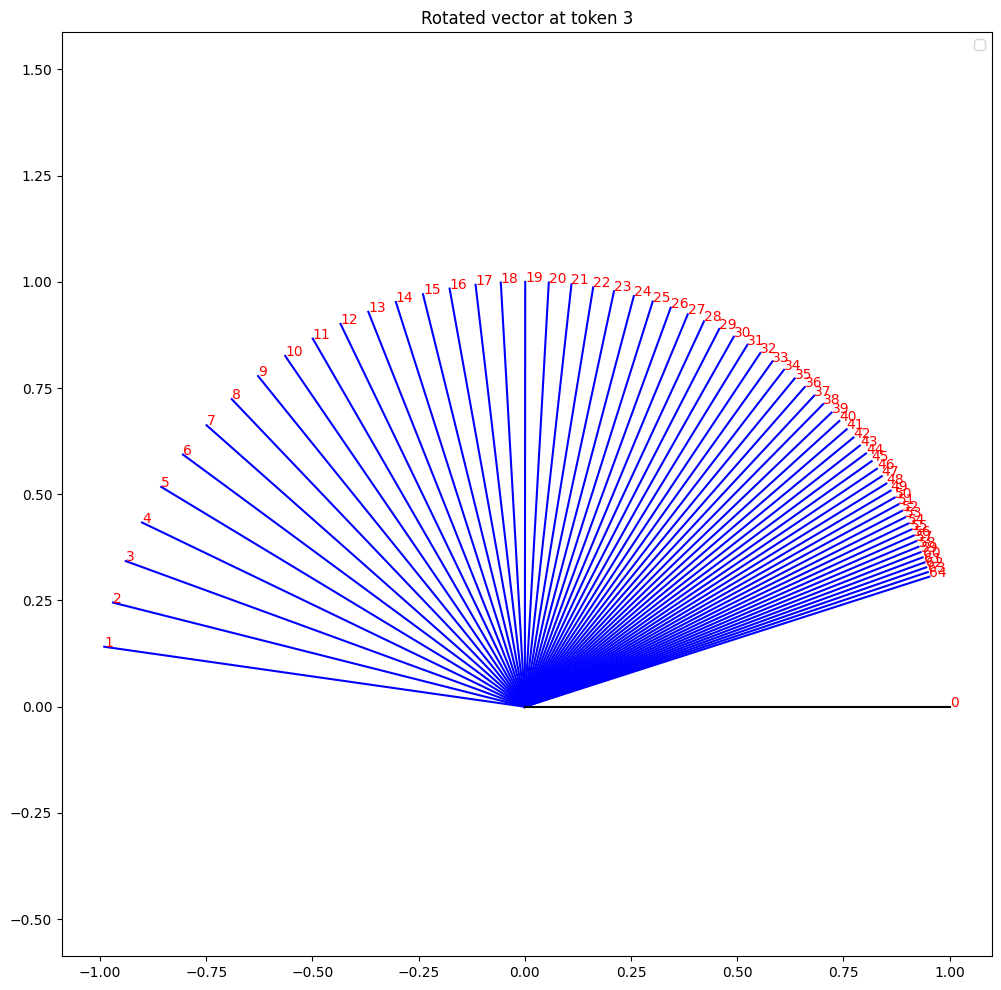
As expected, the initial vector (labeled as 0), is first rotated counter clockwise by an angle of about 171 degrees for the first pair of dimensions, 165 degrees for the second pair, and so on. We don’t show all 256 pairs of dimensions, as they get cluttered, but the pattern is clear.
A question that might arise is:
Are the rotations always monothonic?
No! Let us plot the rotation angles along both the embedding dimensions and the token positions:
plt.figure(figsize=(8, 8))
sns.heatmap(torch.rad2deg(torch.angle(freqs_cis)).cpu().numpy(), cmap='viridis', cbar_kws={'label': 'Rotation Angle (degrees)'})
plt.title('Rotation Angles across Token Positions and Pair Dimensions')
plt.xlabel('Index of pair in embedding dimension')
plt.ylabel('Token Position')
plt.show()
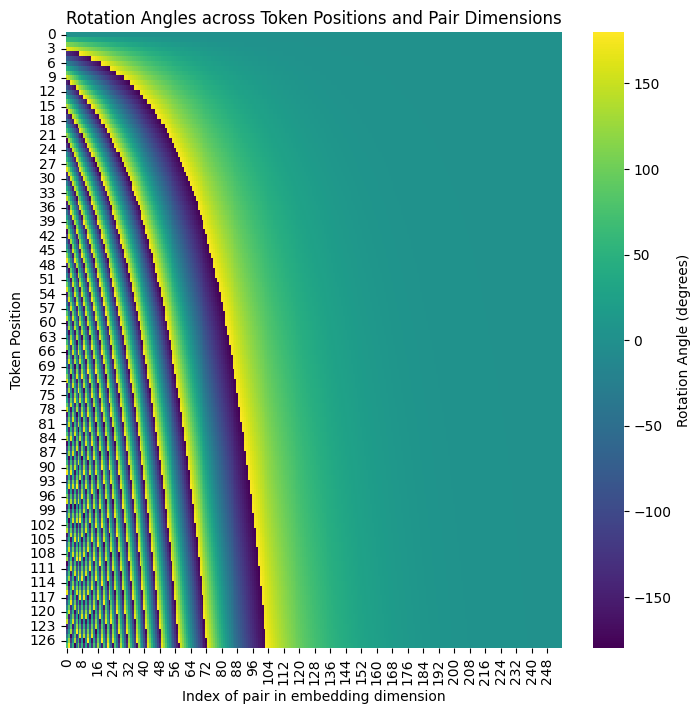
Notice that for many token positions, the rotation angles are not monothonic: they can oscillate between positive and negative values for the angles of rotation.
Extrapolation to longer sequences
Interestingly, it is possible to modify the RoPE mechanism to handle longer sequences than those encountered during training.
Specifically, the mainstream approach to addressing extrapolation with LLMs involves modifying RoPE by replacing $10000$, the base in $10000^{-2(i-1)/d}$ in the original formulation with a larger value and providing longer fine-tuning text.
Sometimes, it is possible to even get away without fine-tuning on longer sequences (see here for an exampling involving LLaMA 3).
The main motivation is to spread out the positional embeddings, making them more distinct for longer sequences.